- Стойността на израза ːx=\left(\sqrt{7}-\sqrt{2}\right)^2-\sqrt{2}\left(\sqrt{2}-2\sqrt{7}\right)ː e:
- Даден е триъгълник със страни 14, 30 и 40. Намерете радиуса на описаната окръжност.
- Стойността на израза ːx=\frac{5}{\sqrt{7}-\sqrt{2}}-\frac{1}{\sqrt{3}-\sqrt{2}}ː е:
- Първият член и разликата на аритметична прогресия, за която a ː_6ː = 0, a ː_{10}ː = 8, са:
- Даден е триъгълник със страни 14, 30 и 40. Намерете най-малката височина на триъгълника.
- Кое от числа e член на числовата редица ːa_n=6n-5ː
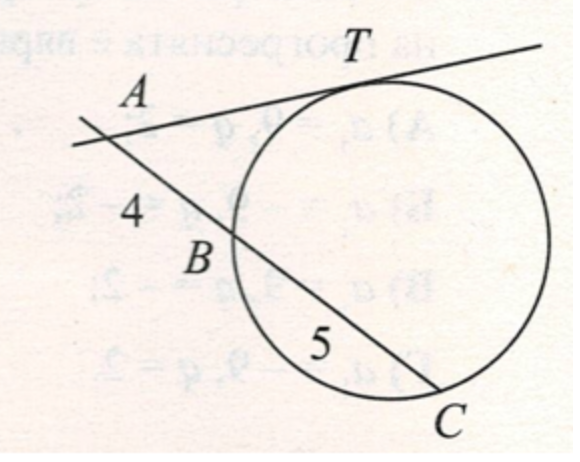
През точка А към окръжност са прекарани допирателни AT и секуща, която отсича хорда ВС от окръжността. Ако АВ=4cm и ВС=5cm, дължината на АТ (в cm) e:
- Седмият член на геометрична прогресия, за която ːa_6=5\ и\ a_8=20ː е:
- Стойността на израза ːx=\frac{3}{\sqrt{5}-\sqrt{2}}-\frac{2}{\sqrt{5}-\sqrt{3}}ː е:
- Корените на уравнението ː3+\sqrt{x-2}=\sqrt{5x+1}ː са:
Математика - 10 клас
Математика - 10 клас
Информация и рейтинг
| Дата: | 2023-12-08 00:16:47 |
| Предмет: | Математика |
| Предназначен за: | Ученици от 10 клас |
| Въпроси: | 10 въпр. |
| Сподели: |
